3. Соединение обмоток генератора треугольником
При соединении обмоток трехфазного генератора треугольником (рис.7.7) конец первой обмотки X соединяется с началом второй обмотки В, конец второй обмотки Y соединяется с началом третьей обмотки С и конец третьей обмотки Z с началом первой А.
Три линейных провода, идущих к приемникам энергии, присоединяются к началам фаз А, В и С.Из рис. 7 ясно, что при таком соединении обмоток фазные напряжения равны линейным, т. е.
Uab = Ua: Ubc = UВ
При соединении треугольником три фазы генератора образуют замкнутый контур с весьма малым сопротивлением. Очевидно, что такое соединение допустимо только в том случае, если сумма ЭДС, действующих в этом контуре, будет равна нулю. Так как в противном случае в контуре даже при отсутствии нагрузки возникнет значительный ток, могущий вызвать перегрев генератора.
Рис.7.Схема соединения обмоток генератора треугольником
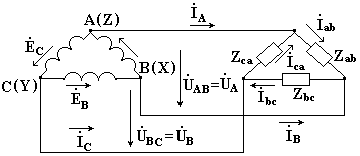
В связи с тем, что значительная часть приемников, включаемых в трехфазные цепи, бывает несимметричной, очень важно на практике, например, в схемах с осветительными приборами, обеспечивать независимость режимов работы отдельных фаз. Кроме четырехпроводной, подобными свойствами обладают и трехпроводные цепи при соединении фаз приемника в треугольник. Но в треугольник также можно соединить и фазы генератора (см. рис. 8).
Для симметричной системы ЭДС имеем Еа + ЕВ + ЕС = 0
Схема соединения фаз генератора и приемника в треугольник представлена на рис. 8, 9.

Рис.8. Рис.9.
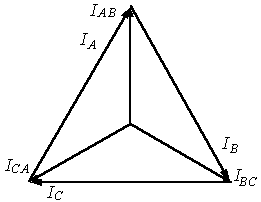 Рис.
10. Диаграмма напряжений и токов по схеме
треугольником
Рис.
10. Диаграмма напряжений и токов по схеме
треугольником
Очевидно, что при соединении в треугольник линейные напряжения равны соответствующим фазным. По первому закону Кирхгофа связь между линейными и фазными токами приемника определяется соотношениями:
Ia = Iab— Ica:
IВ =Ibc —Iab;
Аналогично можно выразить линейные токи через фазные токи генератора.
На рис.10представлена векторная диаграмма симметричной системы линейных и фазных токов: при симметрии токов IЛ = √3IФ
Помимо рассмотренных соединений «звезда — звезда» и «треугольник — треугольник» на практике также применяются схемы «звезда — треугольник» и «треугольник — звезда».
Опасно неправильное соединение обмоток генератора треугольником!
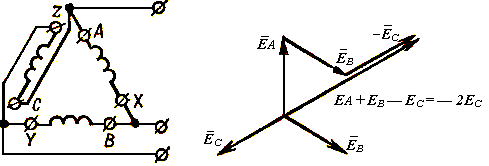
Рис. 11. Неправильная схема соединения обмоток генератора треугольником
Рис. 12. Векторная диаграмма ЭДС генератора, соединенного по схеме рис. 11.
На рис. 11 дана одна из возможных неправильных схем соединения, в которой конец первой фазы X правильно соединен с началом второй фазы В, но конец второй фазы Y соединен не с началом третьей фазы С, а с ее концом Z, и начало третьей фазы С соединено с началом первой фазы А, вследствие чего э. д. с.
Еа + ЕВ — ЕС = — 2ЕС.
Таким образом, в этом случае э. д. с. замкнутого контура по абсолютной величине равна удвоенному значению фазной э. д. с, что при малом сопротивлении контура (обмоток генератора) равносильно
Соединение обмоток генератора треугольником
При соединении обмоток трехфазного генератора треугольником (рис. 7-8) конец первой обмотки X соединяется с началом второй обмотки В, конец второй обмотки У соединяется с началом третьей обмотки С и конец третьей обмотки Z с началом первой А.
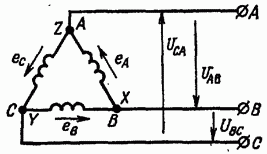
Рис. 7-8. Схема соединения обмоток генератора треугольником.
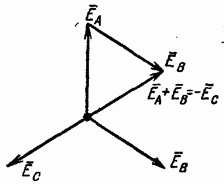
Рис. 7-9. Векторная диаграмма э. д. с. при соединении генератора треугольником.
Три линейных провода, идущих к приемникам энергии, присоединяются к началам фаз А, В и С.
Из рис. 7-8 ясно, что при таком соединении обмоток фазные напряжения равны линейным, т. е.
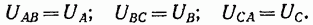
При соединении треугольником три фазы генератора образуют замкнутый контур с весьма малым сопротивлением. Очевидно, такое соединение возможно только в том случае, если сумма э. д. с., действующих в этом контуре, будет равна нулю, так как в противном случае в контуре даже при отсутствии нагрузки возникнет значительный ток, могущий вызвать перегрев генератора.
Сумма трех симметричных э. д. с., действующих в обмотках генератора, равна нулю. В этом легко убедиться, складывая векторы э. д. с.
На
рис. 7-9 даны три вектора э. д. с. Складывая  и
и получаем
вектор, равный и противоположный вектору
получаем
вектор, равный и противоположный вектору

а следовательно, сумма трех векторов э. д. с. равна нулю, т. е.
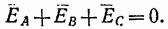
Опасно неправильное соединение обмоток генератора треугольником.
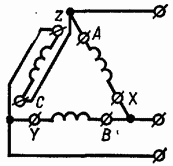
Рис. 7-10. Неправильная схема соединения, обмоток генераторй треугольником.
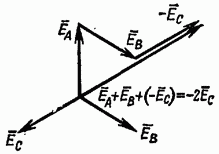
Рис. 7-11. Векторная диаграмма э. д. с. генератора, соединенного по схеме рис. 7-10.
На
рис. 7-10 дана одна из возможных неправильных
схем соединения, в которой конец первой
фазы X правильно соединен с началом
второй фазы В, но конец второй фазы Y
соединен не с началом третьей фазы С, а
с ее концом Z, и начало третьей фазы С
соединено с началом первой фазы А,
вследствие чего э. д. с.  не
складывается с остальными э. д. с., а
вычитается из их суммы. Результирующая
э. д. с. может быть определена из векторной
диаграммы рис. 7-11, на которой произведено
сложение векторов
не
складывается с остальными э. д. с., а
вычитается из их суммы. Результирующая
э. д. с. может быть определена из векторной
диаграммы рис. 7-11, на которой произведено
сложение векторов Сумма
этих трех векторов, как видно из диаграммы,
равна удвоенному вектору
Сумма
этих трех векторов, как видно из диаграммы,
равна удвоенному вектору т.
е.
т.
е.
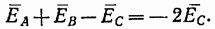
Таким образом, в этом случае э. д. с. замкнутого контура по абсолютной величине равна удвоенному значению фазной э. д. с., что при малом сопротивлении контура (обмоток генератора) равносильно короткому замыканию
13.Векторные диаграммы трехфазной цепи.
На рис. 7.2 изображена векторная диаграмма фазных и линейных напряжений симметричного источника.
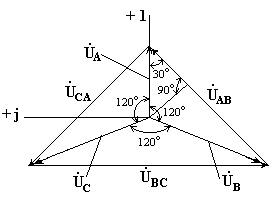 Рис.
7.2
Рис.
7.2
Из векторной диаграммы видно, что
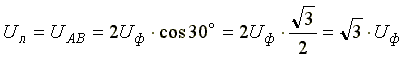
При симметричной системе ЭДС источника линейное напряжение больше фазного в √3 раз.
Uл = √3 Uф
Рис. 7.3
Линейный ток равен геометрической разности соответствующих фазных токов. На рис. 7.4 изображена векторная диаграмма трехфазной цепи, соединенной треугольником при симметричной нагрузке. Нагрузка является симметричной, если сопротивления фаз одинаковы. Векторы фазных токов совпадают по направлению с векторами соответствующих фазных напряжений, так как нагрузка состоит из активных сопротивлений.
 Рис.
7.4
Рис.
7.4
Из векторной диаграммы видно, что
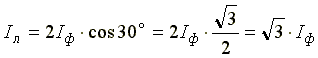 ,
,
Iл = √3 Iф при симметричной нагрузке.
Трехфазные цепи, соединенные звездой, получили большее распространение, чем трехфазные цепи, соединенные треугольником. Это объясняется тем, что, во-первых, в цепи, соединенной звездой, можно получить два напряжения: линейное и фазное. Во-вторых, если фазы обмотки электрической машины, соединенной треугольником, находятся в неодинаковых условиях, в обмотке появляются дополнительные токи, нагружающие ее. Такие токи отсутствуют в фазах электрической машины, соединенных по схеме «звезда». Поэтому на практике избегают соединять обмотки трехфазных электрических машин в треугольник.
На рис. 7.6 изображена векторная диаграмма трехфазной цепи для симметричной нагрузки. 2. Нагрузка несимметричная, RA< RB = RC, но сопротивление нейтрального провода равно нулю: ZN = 0. Напряжение смещения нейтрали

 рис.
7.6
рис.
7.6
Фазные напряжения нагрузки и генератора одинаковы
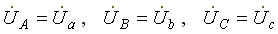
Фазные токи определяются по формулам
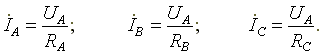
Вектор тока в нейтральном проводе равен геометрической сумме векторов фазных токов.
На
рис. 7.7 приведена векторная
диаграмма трехфазной
цепи, соединенной
звездой, с нейтральным
проводом, имеющим
нулевое сопротивление,
нагрузкой которой
являются неодинаковые
по величине активные
сопротивления.
Рис. 7.7
3. Нагрузка несимметричная,
RA<
RB = RC,
нейтральный провод отсутствует, 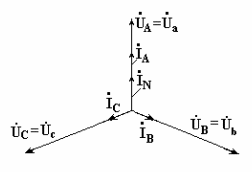
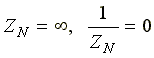
В схеме появляется напряжение смещения нейтрали, вычисляемое по формуле:
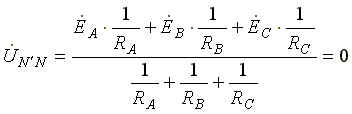
Система фазных напряжений генератора остается симметричной. Это объясняется тем, что источник трехфазных ЭДС имеет практически бесконечно большую мощность. Несимметрия нагрузки не влияет на систему напряжений генератора. Из-за напряжения смещения нейтрали фазные напряжения нагрузки становятся неодинаковыми. Фазные напряжения генератора и нагрузки отличаются друг от друга. При отсутствии нейтрального провода геометрическая сумма фазных токов равна нулю.
На
рис. 7.8 изображена векторная диаграмма
трехфазной цепи с несимметричной
нагрузкой и оборванным нейтральным
проводом. Векторы фазных токов совпадают
по направлению с векторами соответствующих
фазных напряжений нагрузки. Нейтральный
провод с нулевым сопротивлением в схеме
с несимметричной нагрузкой выравнивает
несимметрию фазных напряжений нагрузки,
т.е. с включением данного нейтрального
провода фазные напряжения нагрузки
становятся одинаковыми.
Рис. 7.8 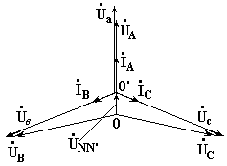
ОБМОТКИ: ЗВЕЗДА И ТРЕУГОЛЬНИК. — СХЕМЫ ОБМОТОК —
ремонт обмоток электрических машин.
СОЕДИНЕНИЕ ОБМОТОК ЗВЕЗДОЙ И ТРЕУГОЛЬНИКОМ.
смотреть статью: ОБОЗНАЧЕНИЕ ВЫВОДОВ ОБМОТОК ЭЛЕКТРОДВИГАТЕЛЕЙ.
СХЕМЫ СОЕДИНЕНИЯ ВЫВОДНЫХ КОНЦОВ ЭЛЕКТРОДВИГАТЕЛЕЙ.
Соединение звездой:
Если фазные обмотки генератора или потребителя соединить так, чтобы концы обмоток были соединены в одну общую точку, а начала обмоток присоединены к линейным проводам, то такое соединение называется соединением звездой и обозначается условным знаком Y. На рис. 1 обмотки генератора и потребителя соединены звездой. Точки, в которых соединены концы фазных обмоток генератора или потребителя, называются соответственно нулевыми точками генератора (0) и потребителя (0’). Обе точки 0 и 0’ соединены проводом, который называется нулевым, или нейтральным проводом. Остальные три провода трехфазной системы, идущие от генератора к потребителю, называются линейными проводами. Таким образом, генератор соединен с потребителем четырьмя проводами. Поэтому эта система называется четырехпроводной системой трехфазного тока.
Рис. 1. Соединение звездой
Сравнивая несвязанную и четырехпроводную системы трехфазного тока, видим, что в первом случае роль обратного провода выполняют три провода системы, а во втором – один нулевой провод. По нулевому проводу протекает ток, равный геометрической сумме токов:
IA, IB и IC, т. е. Ī0= ĪA + ĪB + ĪC.
Напряжения, измеренные между началами фаз генератора (или потребителя) и нулевой точкой (или нулевым проводом), называются фазными напряжениями и обозначаются UA, UB и UC, или в общем виде Uф. Часто задаются величины э.д.с. фазных обмоток генератора. Они обозначаются ЕA, ЕB и ЕC, или Еф. Если пренебречь сопротивлениями обмоток генератора, то можно записать:
ЕA= UA, ЕВ= UВ, ЕC= UС.
Напряжения, измеренные между началами двух фаз: А и В, В и С, С и А – генератора или потребителя, называются линейными напряжениями и обозначаются UАВ, UВС, UСА, или в общем виде Uл. На рис. 1 стрелки показывают выбранное положительное направление тока, которое в линейных проводах принято от генератора к потребителю, а в нулевом проводе – от потребителя к генератору.
Если присоединить зажимы вольтметра к точкам А и В, то он покажет линейное напряжение UАВ. Так как положительные направления фазных напряжений UA, UB и UC выбраны от начал фазных обмоток к их концам, то вектор линейного напряжения UАВ будет равен геометрической разности векторов фазных напряжений UA и UB:
ŪAВ=ŪA— ŪВ.
Аналогично можно записать:
ŪВС=ŪВ— ŪС;
ŪСА=ŪС— ŪА.
Иначе можно сказать, что мгновенное значение линейного напряжения равно разности мгновенных значений соответствующих фазных напряжений. На рис. 2 вычитание векторов заменено сложением векторов:
UA и — UB; UВ и — UС; UС и — UА.
Из векторной диаграммы видно, что векторы линейных напряжений составляют замкнутый треугольник.
Рис. 2. Фазные и линейные напряжения при соединении звездой
Зависимость между линейным и фазным напряжениями:
UBС=2UBcos30o, так как cos30o=√3/2, то UBС=√3UB,
или в общем виде Uл=√3Uф.
Следовательно, при соединении звездой линейное напряжение в √3 раз больше фазного напряжения.
Ток, протекающий по фазной обмотке генератора или потребителя, называется фазным током и обозначается в общем виде Iф. Ток, протекающий по линейному проводу, называется линейным током и обозначается в общем виде Iл. На рис. 1 видно, что при соединении звездой линейный ток равен фазному току, т. е.
Iл=Iф.
Рассмотрим случай, когда нагрузка в фазах потребителя одинакова как по величине, так и по характеру. Такая нагрузка называется равномерной, или симметричной. Это условие выражается равенством.
z1= z2= z3.
Нагрузка не будет равномерной, если, например, z1= r1=0,5ом; z2=ωL2=0,5ом и z3=1/ωC3=0,5ом, так как здесь выполнено лишь одно условие – равенство сопротивлений фаз потребителя по величине, в то время как характер сопротивлений различен (r1 — активное сопротивление, ωL2 — индуктивное сопротивление, 1/ωC3 — емкостное сопротивление).
При симметричной нагрузке:
IА=UА/zА; IВ=UВ/zВ; IС=UС/zС; IА=IВ=IС.
Фазные коэффициенты мощности вследствие равенства сопротивлений и одинаковости их характера будут одинаковы:
cosφ1=rА/zА; cosφ2=rB/zB; cosφ3=rC/zC; cosφ1=cosφ2=cosφ3.
В нулевом проводе должна протекать геометрическая сумма токов всех трех фаз. Если посмотреть на кривые изменения токов при симметричной нагрузке трехфазной системы, то увидим, что максимальные значения для всех трех синусоид тока одинаковы. Поскольку при симметричной нагрузке сумма мгновенных значений токов трехфазной системы равна нулю, следовательно, ток в нулевом проводе будет равен нулю.
Отбрасывая нулевой провод в четырехпроводной системе, переходим к трехпроводной системе трехфазного тока. Если имеется симметричная нагрузка, как, например, трехфазные двигатели переменного тока, трехфазного тока, трехфазные печи, трехфазные трансформаторы и т. п., то к такой нагрузке подводятся только три провода. Потребители, включенные звездой с несимметричной нагрузкой фаз, нуждаются в нулевом проводе.
При симметричной нагрузке фазные напряжения отдельных фаз равны между собой. При несимметричной нагрузке трехфазной системы симметрия токов и напряжений нарушается. Однако в четырехпроводных цепях часто пренебрегают незначительной несимметрией фазных напряжений. В этих случаях между линейными и фазными напряжениями существует зависимость:
Uл=√3Uф.
Соединение треугольником:
Кроме соединения звездой, генераторы, трансформаторы, двигатели и другие потребители трехфазного тока могут включаться треугольником.
Если объединить попарно провода несвязанной шестипроводной системы и соединить фазы, как показано на рисунке 1, получим трехфазную трехпроводную систему, соединенную треугольником.
Рис. 1. Несвязанная трехфазная схема.
Рис. 2. Связанная трехфазная схема, соединенная треугольником.
Соединение треугольником выполняется таким образом (рис. 2), чтобы конец фазы А был соединен с началом фазы В, конец фазы В соединен с началом фазы С и конец фазы С соединен с началом фазы А. К местам соединения фаз присоединяют линейные провода. Если обмотки генератора соединены треугольником, то линейное напряжение создает каждая линейная обмотка. У потребителя, соединенного треугольником, линейное напряжение подключается к зажимам фазного сопротивления. Следовательно, при соединении треугольником фазное напряжение равно линейному: Uл=Uф.
Определим зависимость между фазными и линейными токами при соединении треугольником, если нагрузка фаз будет одинакова по величине и характеру. Составляем уравнения токов по первому закону Кирхгофа для трех узловых точек А1, B1 и C1 потребителя:
ĪA+ ĪСА= ĪАВ;
ĪВ+ ĪАВ= ĪВС;
ĪС+ ĪВС= ĪСА;
откуда
ĪA= ĪАВ—ĪСА;
ĪВ= ĪВС—ĪАВ;
ĪС= ĪСА—ĪВС.
Отсюда видно, что линейные токи равны геометрической разности фазных токов. При симметричной нагрузке фазные токи одинаковы по величине и сдвинуты один относительно другого на 120o. Производя вычитание векторов фазных токов согласно полученным уравнениям, получаем линейные токи. Зависимость между фазными и линейными токами при соединении в треугольник:
Iл=2Iфcos30o=2Iф√3/2=√3Iф.
Следовательно, при симметричной нагрузке, соединенной треугольником, линейный ток в √3 раз больше фазного тока.
У двигателей и у других потребителей трехфазного тока в большинстве случаев наружу выводят все шесть концов обмоток, которые по желанию можно соединять либо звездой, либо треугольником. Обычно к трехфазной машине крепится доска из изоляционного материала (клеммная доска), на которую и выводят все шесть концов.
Если у нас есть двигатель, на паспорте которого написано 127/220 в, значит, этот двигатель можно использовать на два напряжения 127 и 220 в.
Если линейное напряжение сети равно 127 в, то обмотки двигателя необходимо включить треугольником. Тогда на обмотку каждой фазы двигателя будет подано напряжение 127 в. При напряжении 220 в обмотки двигателя нужно включить звездой, тогда обмотка каждой фазы также будет под напряжением 127 в.
Источник:
Соединение фаз генератора и приемника звездой
При соединение фаз обмотки генератора (или трансформатора) звездой их концы X, Y и Z соединяют в одну общую точку N, называемую нейтральной точкой (или нейтралью) (рис. 3.6). Концы фаз приемников (Za, Zb, Zc) также соединяют в одну точку n. Такое соединение называется соединение звезда.
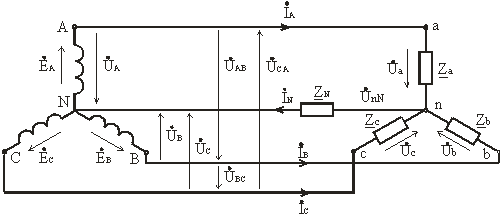
Рис. 3.6
Провода A-a, B-b и C-c, соединяющие начала фаз генератора и приемника, называются линейными, провод N-n, соединяющий точку N генератора с точкой n приемника, – нейтральным.
Трехфазная цепь с нейтральным проводом будет четырехпроводной, без нейтрального провода – трехпроводной.
В трехфазных цепях различают фазные и линейные напряжения. Фазное напряжение UФ – напряжение между началом и концом фазы или между линейным проводом и нейтралью (UA, UB, UC у источника; Ua, Ub, Uc у приемника).Если сопротивлением проводов можно пренебречь, то фазное напряжение в приемнике считают таким же, как и в источнике. (UA = Ua, UB = Ub, UC = Uc). За условно положительные направления фазных напряжений принимают направления от начала к концу фаз.
Линейное напряжение (UЛ) – напряжение между линейными проводами или между одноименными выводами разных фаз (UAB, UBC, UCA). Условно положительные направления линейных напряжений приняты от точек, соответствующих первому индексу, к точкам соответствующим второму индексу (рис. 3.6).
По аналогии с фазными и линейными напряжениями различают также фазные и линейные токи:
При соединении в звезду фазные и линейные токи равны
(3.5)
IФ = IЛ.
Ток, протекающий в нейтральном проводе, обозначают IN.
По первому закону Кирхгофа для нейтральной точки n(N) имеем в комплексной форме
(3.6)
İN = İA + İB + İC.
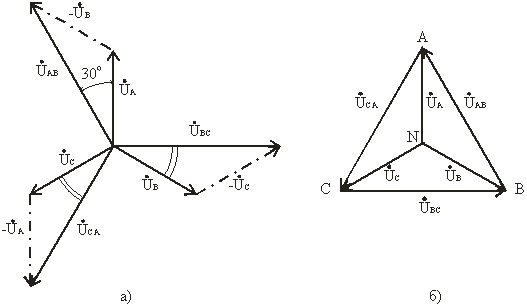
Рис. 3.7
В соответствии с выбранными условными положительными направлениями фазных и линейных напряжений можно записать уравнения по второму закону Кирхгофа.
(3.7)
ÚAB = ÚA — ÚB; ÚBC = ÚB — ÚC; ÚCA = ÚC — ÚA.
Согласно этим выражениям на рис. 3.7а построена векторная диаграмма, из которой видно, что при симметричной системе фазных напряжений система линейных напряжений тоже симметрична: UAB,UBC,UCA равны по величине и сдвинуты по фазе относительно друг друга на 120° (общее обозначение UЛ), и опережают, соответственно, векторы фазных напряжений UA, UB, UC, (UФ) на угол 30°.
Действующие значения линейных напряжений можно определить графи-чески по векторной диаграмме или по формуле (3.8), которая следует из треугольника, образованного векторами двух фазных и одного линейного напряжений:
UЛ = 2 UФ cos 30°
или
UЛ =  UФ.
(3.8)
UФ.
(3.8)
Предусмотренные ГОСТом линейные и фазные напряжения для цепей низкого напряжения связаны между собой соотношениями:
UЛ = 660 В; UФ = 380 В; UЛ = 380 В; UФ = 220 В; UЛ = 220 В; UФ = 127 В.
Векторную диаграмму удобно выполнить топографической (рис. 3.7б), тогда каждой точке цепи соответствует определенная точка на диаграмме. Вектор, проведенный между двумя точками топографической диаграммы, выражает по величине и фазе напряжения между одноименными точками цепи.
Классификация приемников в трехфазной цепи
Приемники, включаемые в трехфазную цепь, могут быть либо однофазными, либо трехфазными. К однофазным приемникам относятся электрические лампы накаливания и другие осветительные приборы, различные бытовые приборы, однофазные двигатели и т.д. К трехфазным приемникам относятся трехфазные асинхронные двигатели и индукционные печи. Обычно комплексные сопротивления фаз трехфазных приемников равны между собой:
(3.9)
Za = Zb = Zc = Zejφ.
Такие приемники называют симметричными. Если это условие не выполняется, то приемники называют несимметричными. При этом, если Za = Zb = Zc, то трехфазный приемник называют равномерным, если φa = φb = φc, то однородным.
Четырехпроводная цепь
Для расчета трехфазной цепи применимы все методы, используемые для расчета линейных цепей. Обычно сопротивления проводов и внутреннее сопротивление генератора меньше сопротивлений приемников, поэтому для упрощения расчетов таких цепей (если не требуется большая точность) сопротивления проводов можно не учитывать (ZЛ = 0, ZN = 0). Тогда фазные напряжения приемника Ua, Ub и Uc будут равны соответственно фазным напряжениям источника электрической энергии(генератора или вторичной обмотки трансформатора), т.е. Ua = UA; Ub = UB; Uc = UC. Если полные комплексные сопротивления фаз приемника равны Za = Zb = Zc, то токи в каждой фазе можно определить по формулам
(3.10)
İa = Úa / Za; İb = Úb / Zb; İc = Úc / Zc.
В соответствии с первым законом Кирхгофа ток в нейтральном проводе
(3.11)
İN = İa + İb + İc = İA + İB + İC.
Симметричная нагрузка приемника
При симметричной системе напряжений и симметричной нагрузке, когда Za = Zb = Zc, т.е. когда Ra = Rb = Rc = Rф и Xa = Xb = Xc = Xф, фазные токи равны по значению и углы сдвига фаз одинаковы
(3.12)
Ia = Ib = Ic = Iф = Uф / Zф,
(3.13)
φa = φb = φc = φ = arctg (Xф/Rф).
Построив векторную диаграмму токов для симметричного приемника (рис. 3.8), легко установить, что геометрическая сумма трех векторов тока равна нулю: İa + İb + İc = 0. Следовательно, в случае симметричной нагрузки ток в нейтральном проводе IN = 0, поэтому необходимость в нейтральном проводе отпадает.
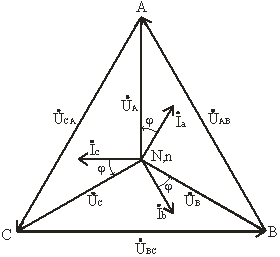
Рис. 3.8
Несимметричная нагрузка приемника
При симметричной системе напряжений и несимметричной нагрузке, когда Za ≠ Zb ≠ Zc и φa ≠ φb ≠ φc токи в фазах потребителя различны и определяются по закону Ома
İa = Úa / Za; İb = Úb / Zb; İc = Úc / Zc.
Ток в нейтральном проводе İN равен геометрической сумме фазных токов
İN = İa + İb + İc.
Напряжения
будут Ua = UA;
Ub = UB;
Uc = UC,
UФ = UЛ / 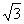 ,
благодаря нейтральному проводу при
ZN = 0.
,
благодаря нейтральному проводу при
ZN = 0.
Следовательно, нейтральный провод обеспечивает симметрию фазных напряжений приемника при несимметричной нагрузке.
Поэтому в четырехпроводную сеть включают однофазные несимметричные нагрузки, например, электрические лампы накаливания. Режим работы каждой фазы нагрузки, находящейся под неизменным фазным напряжением генератора, не будет зависеть от режима работы других фаз.
Векторная диаграмма при несимметричной нагрузке приведена на рис. 3.9

Рис. 3.9
Трехпроводная электрическая цепь
Схема соединения источника и приемника звездой без нейтрального провода приведена на рис. 3.10.
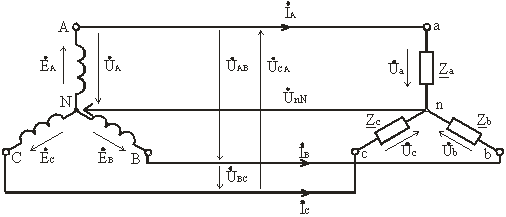
Рис. 3.10
При симметричной нагрузке, когда Za = Zb = Zc = Zφ, напряжение между нейтральной точкой источника N и нейтральной точкой приемника n равно нулю, UnN = 0.
Соотношение
между фазными и линейными напряжениями
приемника также равно 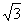 ,
т.е. UФ = UЛ /
,
т.е. UФ = UЛ / 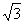 ,
а токи в фазах определяются по тем же
формулам (3.12, 3.13), что и для четырехпроводной
цепи. В случае симметричного приемника
достаточно определить ток только в
одной из фаз. Сдвиг фаз между током и
соответствующим напряжением
φ = arctg (X / R).
,
а токи в фазах определяются по тем же
формулам (3.12, 3.13), что и для четырехпроводной
цепи. В случае симметричного приемника
достаточно определить ток только в
одной из фаз. Сдвиг фаз между током и
соответствующим напряжением
φ = arctg (X / R).
При несимметричной нагрузке Za ≠ Zb ≠ Zc между нейтральными точками приемника и источника электроэнергии возникает напряжение смещения нейтрали UnN.
Для определения напряжения смещения нейтрали можно воспользоваться формулой межузлового напряжения, так как схема рис 3.10 представляет собой схему с двумя узлами,
(3.14)
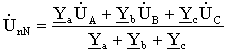 ,
,
где: Ya = 1 / Za; Yb = 1 / Zb; Yc = 1 / Zc – комплексы проводимостей фаз нагрузки.
Очевидно, что теперь напряжения на фазах приемника будут отличаться друг от друга. Из второго закона Кирхгофа следует, что
(3.15)
Úa = ÚA — ÚnN; Úb = ÚB — ÚnN; Úc = ÚC — ÚnN.
Зная фазные напряжения приемника, можно определить фазные токи:
(3.16)
İa = Úa / Za = Ya Úa; İb = Úb / Zb = Yb Úb; İc = Úc / Zc = Yc Úc.
Векторы фазных напряжений можно определить графически, построив векторную (топографическую) диаграмму фазных напряжений источника питания и UnN (рис. 3.11).
При изменении величины (или характера) фазных сопротивлений напряжение смещений нейтрали UnN может изменяться в широких пределах. При этом нейтральная точка приемника n на диаграмме может занимать разные положения, а фазные напряжения приемника Úa, Úb и Úc могут отличаться друг от друга весьма существенно.
Таким образом, при симметричной нагрузке нейтральный провод можно удалить и это не повлияет на фазные напряжения приемника. При несимметричной нагрузке и отсутствии нейтрального провода фазные напряжения нагрузки уже не связаны жестко с фазными напряжениями генератора, так как на нагрузку воздействуют только линейные напряжения генератора. Несимметричная нагрузка в таких условиях вызывает несимметрию ее фазных напряжений Úa, Úb, Úc и смещение ее нейтральной точки n из центра треугольника напряжений (смещение нейтрали).
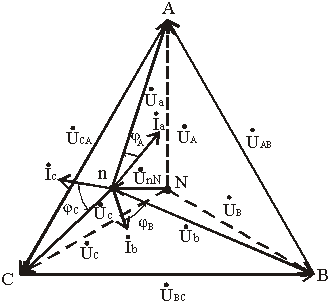
Рис. 3.11
Направление смещения нейтрали зависит от последовательности фаз системы и характера нагрузки.
Поэтому нейтральный провод необходим для того, чтобы:
выравнивать фазные напряжения приемника при несимметричной нагрузке;
подключать к трехфазной цепи однофазные приемники с номинальным напряжением в
 раз
меньше номинального линейного напряжения
сети.
раз
меньше номинального линейного напряжения
сети.
Следует иметь в виду, что в цепь нейтрального провода нельзя ставить предохранитель, так как перегорание предохранителя приведет к разрыву нейтрального провода и появлению значительных перенапряжений на фазах нагрузки.
СОЕДИНЕНИЯ ЗВЕЗДОЙ И ТРЕУГОЛЬНИКОМ — это… Что такое СОЕДИНЕНИЯ ЗВЕЗДОЙ И ТРЕУГОЛЬНИКОМ?
- СОЕДИНЕНИЯ ЗВЕЗДОЙ И ТРЕУГОЛЬНИКОМ
способы соединений элементов электрич. цепей, при к-рых ветви цепи образуют соответственно трёхлучевую звезду и треугольник. Наибольшее распространение С. з. и т. получили в трёхфазных электрич. цепях. При соединении звездой концы обмоток трёх фаз генератора (трансформатора, электродвигателя) объединяются в общую нейтральную точку, а начала обмоток присоединяются к трём отходящим проводам («линейные провода»). При соединении треугольником конец каждой фазы соединяется с началом следующей и к полученным трём узлам присоединяются линейные провода. Если и генератор и приёмник электроэнергии соединены звездой, то нейтр. точки могут быть связаны четвёртым (нейтр.) проводом. У симметричных приёмников, соединённых звездой или треугольником, сопротивления всех трёх фаз одинаковы. В симметричной трёхфазной цепи, соединённой треугольником, напряжения Uл между линейными проводами равны напряжениям Uф на фазах приёмника, а силы тока в линейных проводах в корень из 3 раз больше, чем в фазах приёмника. При соединении звездой линейные напряжения больше фазных в корень из 3 раз, а силы тока в линейных проводах и в фазах одинаковы. См. рис.

Схемы соединений звездой и треугольником трёхфазной (симметричной) цепи: а — звездой; б — треугольником; Uл — линейное напряжение; Uф — фазное напряжение; Iл — сила линейного тока; Iф — сила фазного тока
Большой энциклопедический политехнический словарь. 2004.
- СОЕДИНЕНИЯ
- СОЕДИНИТЕЛЬНАЯ ЛИНИЯ
Смотреть что такое «СОЕДИНЕНИЯ ЗВЕЗДОЙ И ТРЕУГОЛЬНИКОМ» в других словарях:
СОЕДИНЕНИЕ ЗВЕЗДОЙ И ТРЕУГОЛЬНИКОМ — способы соединений, применяемые в трехфазной электрической цепи (рис. С 15). При соединении звездой концы обмоток трех фаз генератора (трансформатора, электродвигателя) соединяют в общую нейтральную точку, а начала обмоток присоединяют к трем… … Металлургический словарь
Треугольником и звездой соединения — в электротехнике, способы соединения элементов электрических цепей (См. Электрическая цепь), при которых ветви цепи образуют соответственно треугольник и трехлучевую звезду (см. рис.). Наибольшее распространение Т. и з. с. получили в… … Большая советская энциклопедия
Трёхфазная цепь — трёхфазная система, совокупность трёх однофазных электрических цепей переменного тока (См. Переменный ток) (называемых фазами), в которых действуют три переменных напряжения одинаковой частоты, сдвинутых по фазе друг относительно друга;… … Большая советская энциклопедия
Электродвигатели — Попытки применить электричество как двигательную силу были сделаны еще в начале прошлого столетия. Так, после того как (1821 г.) Фарадеем было открыто явление вращения магнитов вокруг проводников с токами и наоборот, Sturgeons и Barlow построили… … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона
Сельсин — (англ. selsyn, от англ. self сам и греч. sýnchronos одновременный, синхронный) Электрическая машина, позволяющая осуществлять угловое перемещение вала какого либо устройства или механизма в соответствии с угловым перемещением другого вала … Большая советская энциклопедия
Электрическая канализация — Э. канализация представляет собой ряд приспособлений и сооружений для распределения Э. энергии от данного источника к приемникам, расположенным в разных пунктах данной местности. Главной частью Э. канализации являются провода, по которым… … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона
Трансформатор — У этого термина существуют и другие значения, см. Трансформатор (значения). Трансформатор силовой ОСМ 0,16 Однофазный сухой многоцелевого назначения мощностью 0.16 кВт … Википедия
Выпрямитель — У этого термина существуют и другие значения, см. Выпрямитель (значения) … Википедия
Диодный выпрямитель — Выпрямитель электрического тока механическое, электровакуумное, полупроводниковое или другое устройство, предназначенное для преобразования переменного входного электрического тока в постоянный выходной электрический ток.[1] [2] Большинство… … Википедия
Трёхфазная система электроснабжения — Трёхфазная система электроснабжения частный случай многофазных систем электрических цепей, в которых действуют созданные общим источником синусоидальные ЭДС одинаковой частоты, сдвинутые друг относительно друга во времени на определённый… … Википедия




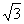 раз
меньше номинального линейного напряжения
сети.
раз
меньше номинального линейного напряжения
сети.